構造上の特長

CLEFIAでは、すでに確立されている共通鍵ブロック暗号の伝統的な設計技法と、今回導入したいくつかの新しい設計技法とを巧みに融合することで、優れた性能を達成しています。これをいくつかの設計上のポイントをあげながら紹介いたします。

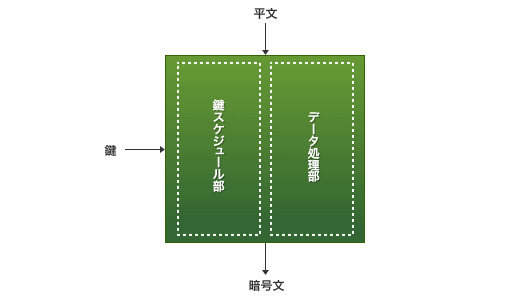
一般的に、共通鍵ブロック暗号はデータ処理部と鍵スケジュール部に分けて考えることができます。CLEFIAの設計上の特長の第1として挙げられるのはこのデータ処理部の基本構造です。

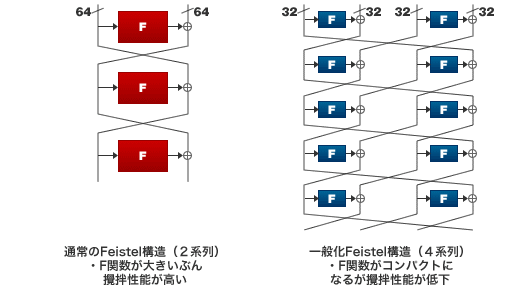
CLEFIAでは通常2系列であるFeistel構造を4系列に拡張した一般化Feistel構造を採用しています。さらにひとつのラウンドに32ビット入出力を持つ2つのF関数を並列に配置した構造を選んでいます。

このような構造を選択することで、1つ1つのF関数のサイズを通常の2系列を持つFeistel構造と比べて小さくすることが可能になります。これによりコンパクトなF関数の実装が容易になることが期待されます。

しかしながら一般的には、F関数のサイズが小さくなるにつれて、期待される攪拌性能が落ちてしまう傾向があります。そのため、安全性を確保するには必要な繰り返し処理数を増やさなければいけませんでした。このことからこれまでは、一般化Feistel構造は、通常のFeistel構造と比較して採用されにくかったと考えられます。

一方、近年Feistel構造において、差分攻撃と線形攻撃への耐性を向上させるための技術が新しく登場し研究されてきました。差分攻撃と線形攻撃は、共通鍵ブロック暗号に対する代表的な攻撃法であり、非常に強力な攻撃法です。

この技術は拡散行列切り替え法（Diffusion Switching Mechanism, 以下DSM）と呼ばれています。DSMを用いると両攻撃に対する安全性を飛躍的に高められ、十分な安全性を少ない繰り返し回数で確保できます。つまりDSMを用いることで高速な暗号化関数を作ることが可能になります。しかしながらDSMを通常の2系列のFeistel構造に適用した場合には、複数の行列を切り替えて使用するため実装コストが増大してしまうという懸念がありました。

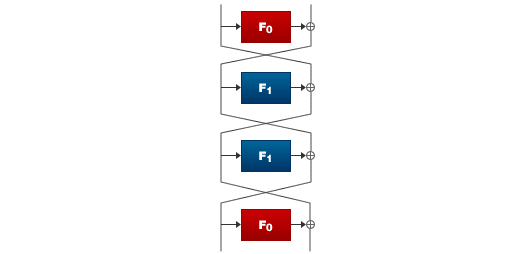
CLEFIAでは、4系列の一般化Feistel構造にDSMを採用することで、両技術の相乗効果によりコンパクト性と高速性を両立することに成功いたしました。具体的には2つの異なる行列を同一ラウンド内にある2つのF関数に配置しました。こうすることでDSMの効果が得られつつ、かつラウンド関数は同一の処理の繰り返し構造となっているため、実装コストを増大させることなく実行させることが可能になりました。結果、DSMを採用しない方法と比較して7割程度の繰り返し処理で安全性を保つことが可能になり、高速な暗号化関数を構成することに成功しました。

CLEFIAの構造上の主な特長は以上のようなものですが、CLEFIAでは、さらに鍵スケジュール部やF関数内部のコンポーネントを実装に適するように設計しています。次のページにて、これらの設計技術について説明いたします。